Brief

Defining Recursion

In general, recursion is defined as the repeated application of a recursive procedure. In computer science, it is a programming technique involving the use of a function that calls itself one or more times until a specific condition is met (commonly known as the base case). Concretely, it is a method of solving a problem where the solution depends on solutions to smaller instances of the same problem.

Prototyping

A recursive function has one or more base cases and one or more recursive calls.

A recursive call is a portion of the function that calls itself in order to get closer to solving the problem.

A base case is a condition which, if met, will cease further recursive calls.

The following pseudocode represents a typical format for a recursive function:

foo(/*params...*/)
{
    //Base step(s)
        //Return value(s) that doesn’t call foo()
        //This is the value(s) we are in some way approaching
	
    //Recursive step(s)
        //Return value(s) that does call foo()
        //Move the value(s) in the foo() call towards the base case
}

Factorial

A factorial is the product of an integer and all the integers below it. For example, factorial for 4 (denoted as 4!) is equal to 4*3*2*1 = 24. The code below is a recursive function definition for calculating a factorial.

int factorial(int n) {
    // Recursive call
    if(n > 1) {
        return n * factorial(n - 1);
    }
    // Base case
    return 1;
}

If one were to make the function call factorial(4), the function would execute like the following:

1. First it calculates factorial(4). Since n = 4, the recursive case is true. Therefore factorial(4) equals 4 * factorial(3). But now it needs to calculate factorial(3) to finish the problem.
2. It then calculates factorial(3). Since n = 3, the recursive case is true. Therefore factorial(3) equals 3 * factorial(2). But now it needs to calculate factorial(2) to finish the problem.
3. factorial(2) is then calculated. Since n = 2, the recursive case is true. Therefore factorial(2) equals 2 * factorial(1). But now it needs to calculate factorial(1) to finish the problem.
4. Finally, it calculates factorial(1). Since n = 1, the base case is true. Therefore factorial(1) equals 1. We’ve reached an endpoint and are now able to calculate factorial(2) completely to finish the problem.
5. Since the value of factorial(1) is 1, the calculation in step 3 for factorial(2) can finish. factorial(2) = 2*1 = 2.
6. Now that it knows that the value of factorial(2) is 2, the calculation in step 2 for factorial(3) can finish. factorial(3) = 3*2 = 6
7. And finally, since factorial(3) is 6, the calculation in step 1 for factorial(4) can finish. factorial(4) = 4*6 = 24.

Fibonacci

Another popular function is the recursive fibonacci. The Fibonacci series is a series of numbers in which each number is the sum of the two preceding numbers. Ex. 1, 1, 2, 3, 5, 8, etc. The fourth fibonacci number in this series if 3.

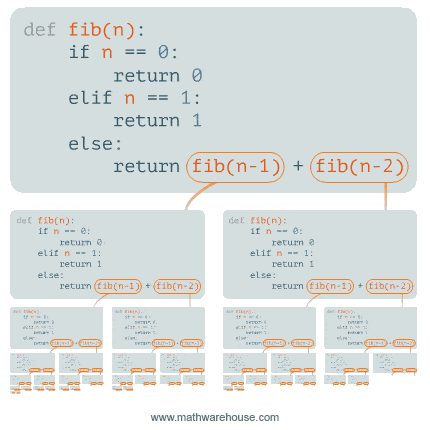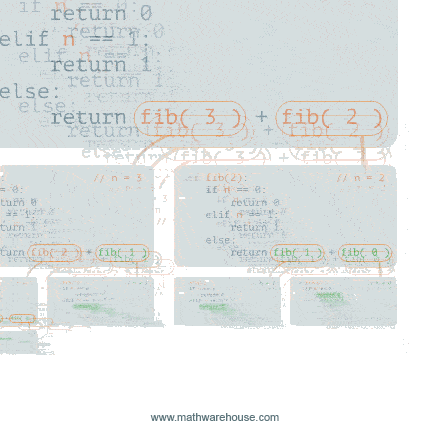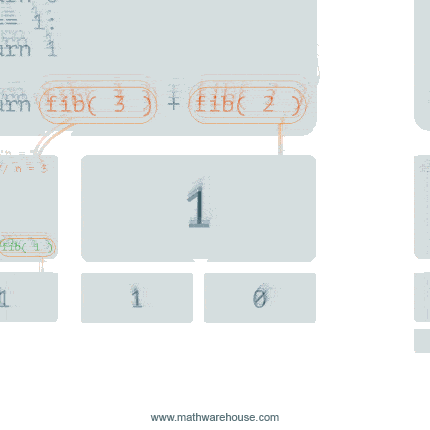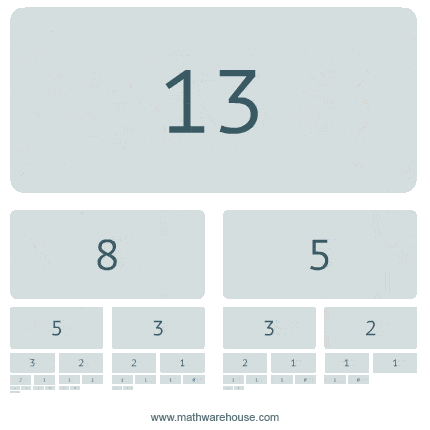
The code below is a recursive function definition for calculating the nth fibonacci number.

int fib(int n) {
    // Base case
    if(n == 1 || n == 2) {
        return 1;
    }

    // Recursive call
    return fib(n - 1) + fib(n - 2);
}

Walk through the each line of code and see why it works.