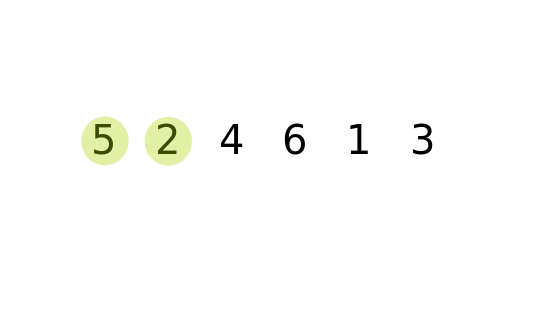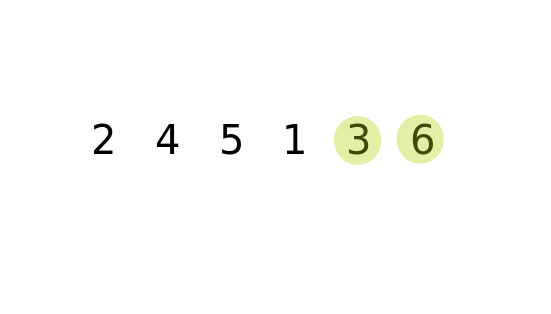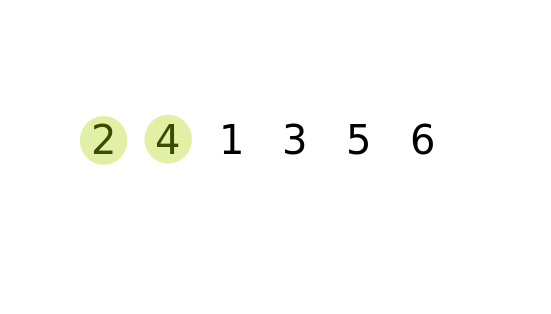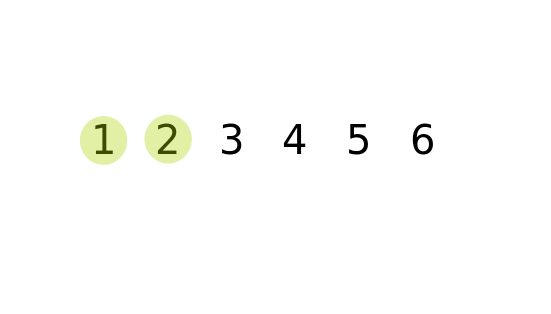Brief
Array Basics
An array is a collection of elements of the same data type placed in a contiguous block of memory. Each element in the array can be referenced by its index. An array’s index has the range of 0 to N-1, where N is the number of elements the array can hold.
It is important to note that an array’s capacity is a constant; it cannot be made larger or smaller. If one wishes to store more data than an array can hold, one would have to allocate a larger array and copy the contents of the smaller array into the larger one.
Let’s take a look at the example below.
double f[5];
int m[10];
f[4] = 2.5;
m[2] = 4;
cout << f[m[2]];The lines double f[5] and int m[10], respectively, allocate an array of floating point numbers whose capacity is 5 and an array of integers whose capacity is 10.
We then assign 2.5 to the fourth element of the array f and 4 to the second element of the m. The resulting arrays are:
f
| INDEX | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| ELEMENT | - | - | - | - | 2.5 |
m
| INDEX | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| ELEMENT | - | - | 4 | - | - | - | - | - | - | - |
The final line, cout << f[m[2]] outputs the fourth element of f.
You are able to initialize arrays. Let’s take a look on how to do so.
int a[] = {10, 11, 12, 13};
bool b[] = {false, true};
char c[] = {'c', 'a', 't'};The resulting arrays look like this:
a
| INDEX | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| ELEMENT | 10 | 11 | 12 | 13 |
b
| INDEX | 0 | 1 |
|---|---|---|
| ELEMENT | false | true |
c
| INDEX | 0 | 1 | 2 |
|---|---|---|---|
| ELEMENT | c | a | t |
Bubble Sort
As a warm up let’s take a look at the bubble sort algorithm and walk through it line-by-line.
void BubbleSort(int *arr, const int kSize) {
for (int i = kSize; i > 0; i--) {
for (int j = 0; j < i - 1; j++) {
if (arr[j] > arr[j + 1]) {
int temp = arr[j + 1];
arr[j + 1] = arr[j];
arr[j] = temp;
}
}
}Before we describe the code, let’s visualize the sorting algorithm first.
The algorithm searches through the array in pairs, and swaps elements that are out of order. Naturally, this moves the largest element to the end of the array during the first iteration, the second largest element during the second iteration, etc. Therefore, after the kth iteration of the search, you only have to search through the N-k elements, where N represents the size of the array.
The outer loop for(int i = kSize; i > 0; i--) is responsible for keeping track of how many elements need to be searched through. The inner loop for (int j = 0; j < i - 1; j++) is used to iterate through the elements that are left. The elements are then swapped if they are out of order. In this case, the elements are swapped if the next element is smaller than the previous.